Binary Tree Level Order Traversal: Step-by-Step Guide

Level order traversal is one of the most intuitive and useful ways to explore a binary tree. Instead of following a single branch deep into the tree (like preorder, inorder, or postorder traversal), level order visits each level from top to bottom, left to right.

This traversal is often called breadth-first traversal (BFS) because it explores all nodes at the current depth before moving to the next level.

Why Level Order Traversal?

• Helps visualize the tree structure clearly.
• Useful in tree serialization and deserialization.
• Forms the basis for solving various algorithmic problems, such as finding the shortest path or checking whether a tree is complete.

Algorithm Overview

A standard way to implement level order traversal uses a queue:

1. Start by adding the root node to the queue.

2. While the queue is not empty:

   • Remove the node at the front of the queue.
   • Process it (for example, add its value to a list).
   • Add its left and right children to the queue if they exist.
   • Continue until all nodes have been processed.

This ensures that nodes are visited level by level.

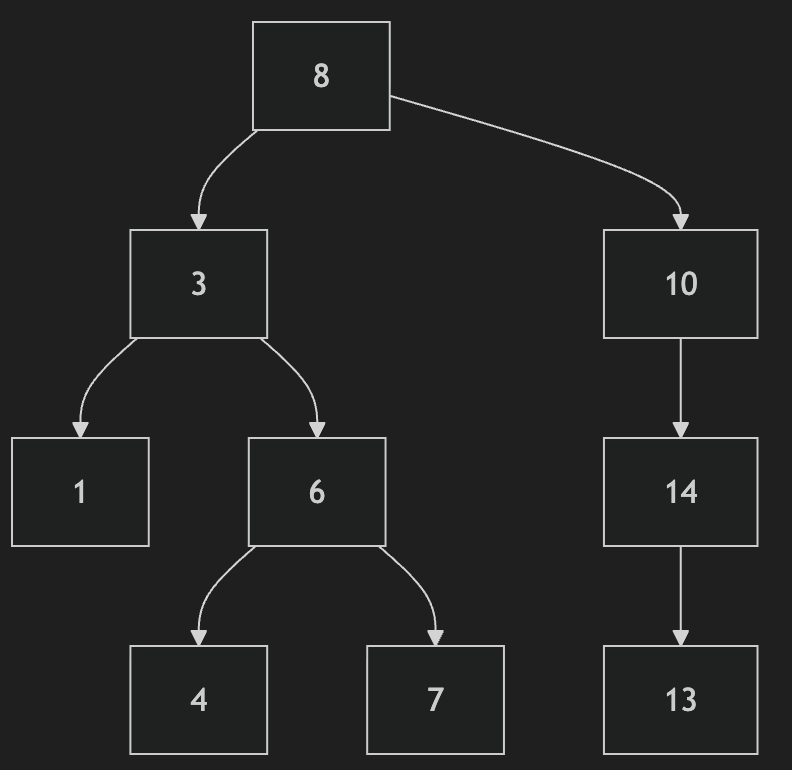
Python Example

Let’s look at a Python implementation of level order traversal.

from collections import deque

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def level_order_traversal(root):
    """
    Returns the level order traversal of a binary tree as a list of lists.
    Each sublist contains values at that level.
    """
    if not root:
        return []

    result = []
    queue = deque([root])

    while queue:
        level_size = len(queue)
        level = []

        for _ in range(level_size):
            node = queue.popleft()
            level.append(node.val)

            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

        result.append(level)

    return result

Writing Tests

It’s important to write tests to confirm that the implementation behaves as expected.

def test_level_order_traversal():
    # Build the following tree:
    #      1
    #     / \
    #    2   3
    #   / \   \
    #  4   5   6
    root = TreeNode(1)
    root.left = TreeNode(2, TreeNode(4), TreeNode(5))
    root.right = TreeNode(3, None, TreeNode(6))

    expected = [
        [1],
        [2, 3],
        [4, 5, 6]
    ]

    result = level_order_traversal(root)
    assert result == expected, f"Expected {expected}, but got {result}"

def test_empty_tree():
    assert level_order_traversal(None) == []

def test_single_node():
    root = TreeNode(42)
    assert level_order_traversal(root) == [[42]]

if __name__ == "__main__":
    test_level_order_traversal()
    test_empty_tree()
    test_single_node()
    print("All tests passed!")

Complexity Analysis

Where n is the number of nodes in the tree. We visit each node exactly once, and in the worst case, the queue may hold up to n nodes.

Conclusion

Level order traversal is a straightforward yet powerful way to explore binary trees. It helps reveal the structure of the tree clearly and is fundamental to solving many tree-based problems. Using a queue keeps the implementation clean, and writing tests ensures correctness in real-world scenarios.